Pas toujours évident de se repérer parmi les 3 axes d’une imprimantes 3D de type cartésien. Et qu’en est-il de la spatialité d’une imprimante delta ? Comment ça marche ? C’est dans cet article que je vais tenter de répondre à la majorité des questions que l’on se pose lorsqu’on monte, améliore ou bidouille une imprimante 3D !

Se repérer dans l’espace – notions de mathématiques

Avant de commencer, il est important de faire un petit point sur les notions de coordonnées cartésiennes et de coordonnées polaires. Je vais simplifier au maximum les explications, ce n’est pas un cours sur les mathématiques ! x)

On va tout d’abord commencer par un espace à 2 dimensions. Pour situer un point sur une grille, on peut utiliser ses coordonnées cartésiennes en le situant dans l’espace sur repère orthonormé. Exemple ici :

Ici, c’est comme au jeu de la bataille navale. On voit que notre point est en (3,2). Les coordonnées représentent effectivement la position du point respectivement par rapport aux axes XY. Cette notion de coordonnées cartésiennes est utilisée sur les imprimantes dites cartésiennes.

Il y a également une seconde manière de représenter les coordonnées : de manière polaire. Dans un espace à 2 dimensions, les coordonnées sont représentées respectivement par la distance du point à l’origine et l’angle formé par le segment origine/point et l’axe origine. L’axe origine peut être délibérément choisi.

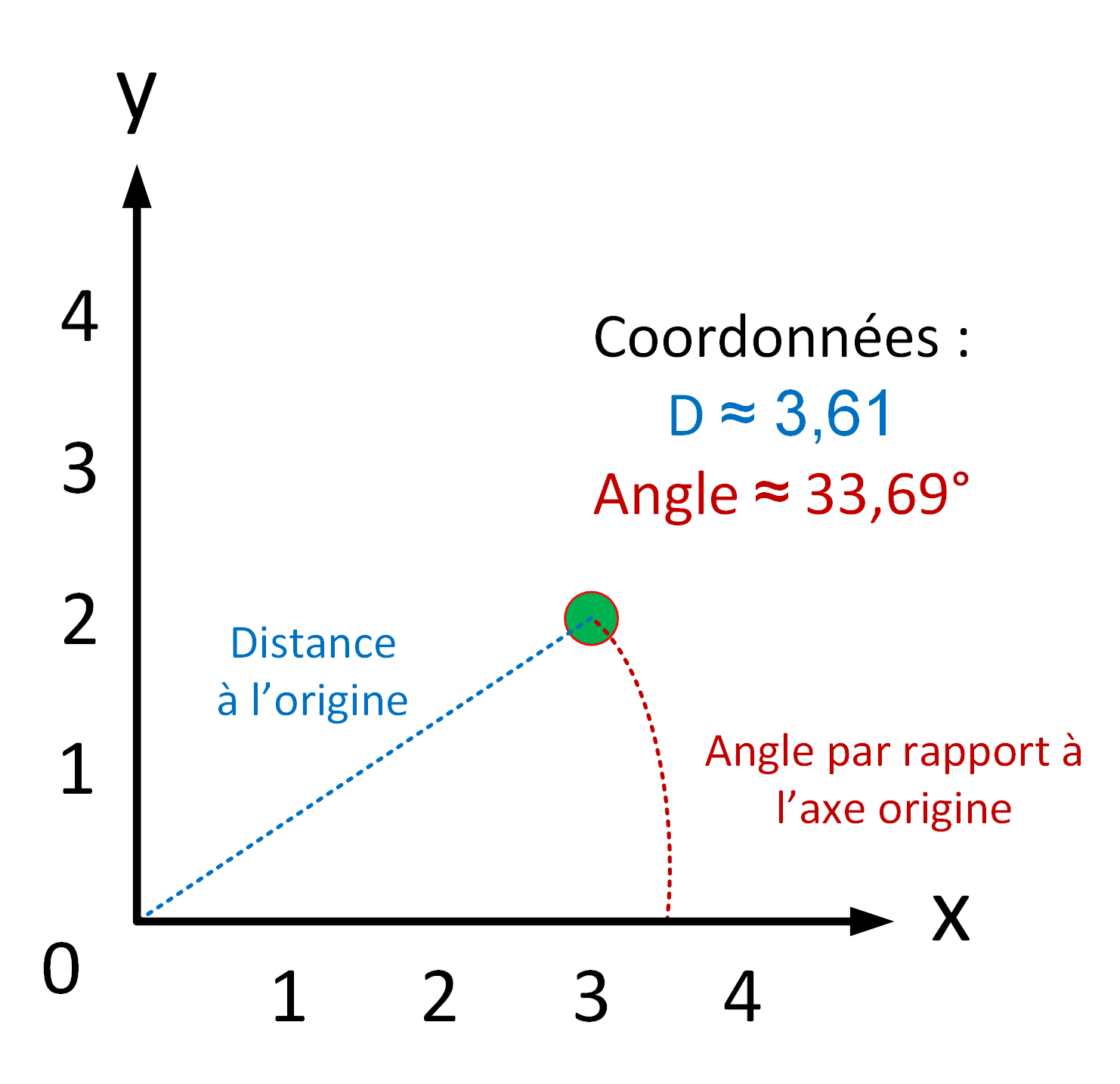
Si on reprend le même point que tout à l’heure, on retrouve grâce au théorème de Pythagore la distance du point à l’origine qui est de 3,62. Pour trouver l’angle, on utilise l’inverse du cosinus du rapport côté adjacent sur l’hypoténuse. Soit cos^-1(3/3,61). Ce qui nous donne un angle de 33,69°.

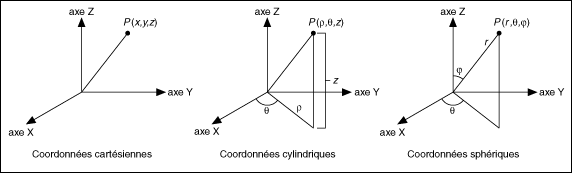
Maintenant, plaçons-nous dans un espace à 3 dimensions. De la même manière, on pourra placer un point dans l’espace grâce aux coordonnées cartésiennes. On ne parle plus de représentation polaire en 3 dimensions, mais de coordonnées cylindriques ou sphériques. Cette fois-ci, on repérera les données cartésiennes selon 3 axes, et donc 3 coordonnées au lieu de 2. Pour les coordonnées sphériques, les coordonnées seront définies avec la distance du point à l’origine et 2 angles. Pour les coordonnées cylindriques, il s’agira de la distance à l’origine, de la distance à l’origine du point projeté sur le plan origine et de l’angle formé entre le segment origine-point et le plan origine.

Les axes sur les imprimantes cartésiennes

Sur une imprimante cartésienne, les axes d’une imprimantes 3D sont définies de la manière suivante :

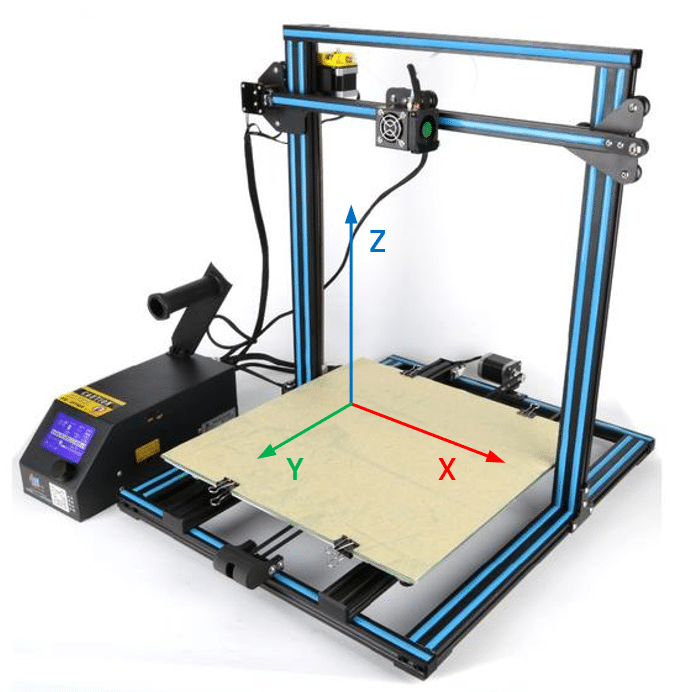
Lorsque l’imprimante va se mettre à imprimer, elle va décrypter un code, plus communément appelé Gcode. Il s’agit d’un code compris et interprété par la carte de la machine. Si on regarde ce code de plus près, ce dernier fonctionne couche par couche. L’imprimante imprime donc en 2D la plupart du temps (logique, mais bon, ça se confirme sur le Gcode :-D).

Extrait d’un Gcode issu de Cura pour Dagoma DiscoEasy 200 (badge Dagoma)

En effet, au lieu de donner l’ordre à l’imprimante d’aller en XYZ à chaque ligne, pour diminuer le nombre d’instructions le gcode est optimisé. Le Z n’est pas tout le temps spécifié (car on reste à la même hauteur pour une même couche, logique ^^). Il y a également le paramètre E qui rentre en compte et qui définit la vitesse d’extrusion du plastique. Les ordres sont donc du type :

Va en couche n°Z position XY vitesse d’extrusion E
Va en position XY vitesse d’extrusion E
Va en position XY vitesse d’extrusion E
Va en position XY vitesse d’extrusion E
Va en position XY vitesse d’extrusion E
Va en couche n°Z position XY vitesse d’extrusion E
Va en position XY vitesse d’extrusion E
Va en position XY vitesse d’extrusion E
Va en position XY vitesse d’extrusion E
Va en position XY vitesse d’extrusion E

Les axes sur les imprimantes Delta

Mais pour les imprimantes delta ? A quoi le gcode ressemble-t-il ? Est-il différent ? Et bien la réponse est que pas vraiment, non ! En fait, la structure du Gcode est exactement la même que pour une imprimante cartésienne. Les ordres vont être semblables à la différence près que les coordonnées ne seront pas identiques pour une même pièce, car la surface d’impression sera rarement la même ! J’y suis allé de ma propre expérience en prenant les deux imprimantes de chez Dagoma : la NEVA (Delta) et la DiscoEasy 200 (Cartésienne). J’ai téléchargé leur slicers respectifs officiels : Cura by Dagoma for DiscoEasy 200 et Cura by Dagoma for NEVA. J’ai généré le Gcode avec la même pièce et les mêmes paramètres d’impression de chaque côté.

Mis à part les coordonnées qui ont été ajustés et quelques fonctions en + côtés NEVA, la structure du Gcode est identique.

Et c’est là où c’est très intéressant, car les imprimantes Delta, tout comme les imprimantes cartésiennes possèdent un firmware, un progiciel installé dans leur carte. Dans ce firmware, de nombreuses variables y sont paramétrées. Il y a notamment des variables permettant de passer des ordres donnés par le Gcode à la réalité. Transformer les positions XYZ en consigne à donner aux trois moteurs. C’est avec ces variables qu’un calcul sera effectué pour passer d’une position XYZ à une consigne moteur. Dans ces variables on retrouve des variables comme :

• La longueur des bras,
• L’angle minimal possible de chaque bras,
• Un offset angulaire,
• L’offset Z,
• Une valeur de correction angulaire par tour,
• Etc…

C’est donc là, dans le firmware, que les coordonnées XYZ données par le Gcode vont être passé en coordonnée sphériques ou cylindrique (dépends des firmwares), puis adaptées en signaux pour chaque moteur afin que la course de chaque moteur puisse créer un angle bras / structure adapté aux coordonnées demandées. Je trouve que cette complexité du ballet exercé par ces trois axes angulaires fait de ces imprimantes 3D des machines incroyables et vraiment classes !

En résumé, les trois axes XYZ peuvent être représentés de cette manière sur une imprimante delta :

Ben.